今年のノーベル化学賞の受賞者はダニエル・シェヒトマン博士。1984年に初めてアルミニウム-マンガン(Al-Mn)合金から「準結晶」を発見したイスラエルの化学者です。(なお、この記事は大西将徳と田端萌子の共同執筆です)。
さて、準結晶とは一体何なのでしょうか。それを理解するためには「結晶」とは何かを知る必要があります。
結晶の条件は「原子や分子が規則正しく立体的に配列されていること」。ここでの「規則正しく」は、横にずらしたり(並進)、回転させたりしても元の形とぴったり重なることを指します。今回注目すべきは、回転させても元の形と重なるという回転対称性。
回転対称の考え方
直方体の真ん中に串を刺します。その串の周りに直方体を180°回転させると元の形とぴったりと重なります。もう180°回転させると完全に元の状態に戻るのでこれを「2回対称」といいます。
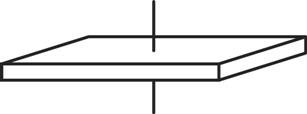
正三角柱の真ん中に串が刺さったものを串の周りに120°回転させると、元の形とぴったりと重なります。これを3回繰り返すと完全に元の状態に戻るのでこれを「3回対称」といいます。
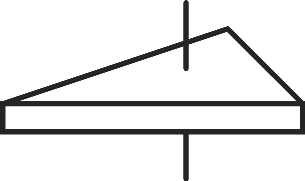
正四角柱を真ん中の串の周りに90°回転させると、元のかたちとぴったり重なり、これを4回繰り返すと、完全に元の状態に戻るので「4回対称」といいます。
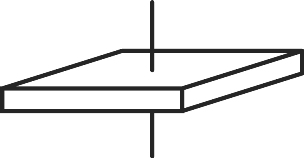
正六角柱も同様に考えると60°回転させると元の形とぴったりと重なり、6回繰り返すと元の状態に戻る「6回対称」。
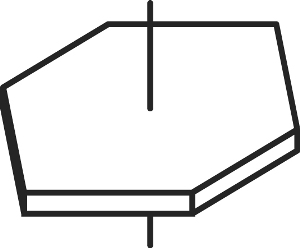
結晶には以上の2,3,4,6回転対称しか存在しえません。あれ?5回対称も8回対称もあるんじゃないの、と思われた方がいるかもしれません。確かにひとつの単位で考えるとそれも可能ですが、結晶はこのようなひとつの単位が3次元的に無限に配列されたもの。納得いかない!という方は絵に描いて考えてみてください。
準結晶のどこがすごい?
1984年ダニエル・シェヒトマン博士は電子線回折によって、結晶にはありえない5回対称性を示す合金を発見しました。これは、5回対称の規則正しく立体的に配列された形が存在するという意味ではありません。細かいところではぴったりと重ならない部分があり、全体的には秩序を持っているという意味です。
ずらしたり回転させたりして一致するという「規則正しさ」は私たちが実際に目で見て確かめられる「秩序」ですが、準結晶に見られる「秩序」は私たちの理解を超えたものであるようです。
我々人間は自然界で起こっている事象を理解するために物理や数学を使い、説明をします。しかし物理や数学を使うと、例えば光は粒子であり波であると説明できますが、果たしてその実態を理解していると言えるのでしょうか。我々が理解してきた物事は、実は自然のほんの一側面に過ぎないのかもしれないのです。今回の発見は、自然界には人間の理解を超えるようなことがあり、その奥深さを垣間見せてくれたものと言えるでしょう。
※ 2人で熟議をしていたらこんなに遅くなりました。今、夜中の1時です。
(大西将徳、田端萌子)
<管理人による修正>
下記コメント欄にあるご指摘を受け、正三角柱、正六角柱の角度を直しました。







