
こんにちは。福田大展です。私は「ノーベル物理学賞」を予想したいと思います。実はこの賞には規則性があると噂されております。「物性、宇宙、物性、素粒子、物性・・・」。物性が2年おきに受賞し、間の年は宇宙と素粒子が交互に選ばれるらしいのです。というわけで、過去10年の受賞歴を振り返ってみましょう。

確かに!限りなく規則性に従っていますね!という訳で、私が予想する今年のノーベル物理学賞は、これ!
「素粒子!」
問題は、素粒子のどのテーマが受賞するかです。素粒子といえば、昨年世間を騒がせた大ニュースがありましたよね。「ヒッグス粒子の発見」。今年のノーベル物理学賞はヒッグスで決まり。そんな前評判がすごいですが、今回はあえて外したいと思います!(キリッ)私の予想はこれです!
福田の予想する物理学賞
トップクォークの発見

ポール・グラニス(75)
(ニューヨーク州立大学名誉教授)
1938年生まれ。1983年からフェルミ加速器研究所の「D0(ディーゼロ)」実験にリーダーとして参加。実験の設計から携わり、1995年にトップクォークを発見した。2001年、素粒子実験物理学の功績をたたえるパノフスキー賞を受賞。

Mel Shochet
(シカゴ大学 エンリコ・フェルミ研究所名誉教授)
フェルミ加速器研究所の「CDF」実験にリーダーとして参加。1995年にトップクォークを発見した。
トップクォークって何?
ノーベル賞候補になるくらいなので、トップクォーク(以下「トップ」)とやらは、さぞかしすごいものなのだろうと思いますよね。トップとは、この世の物質をつくる最小の粒々「素粒子」のひとつなんです。「最小」なので数が少ないと思いきや、そういう粒々は結構たくさんの種類があるんですよ。
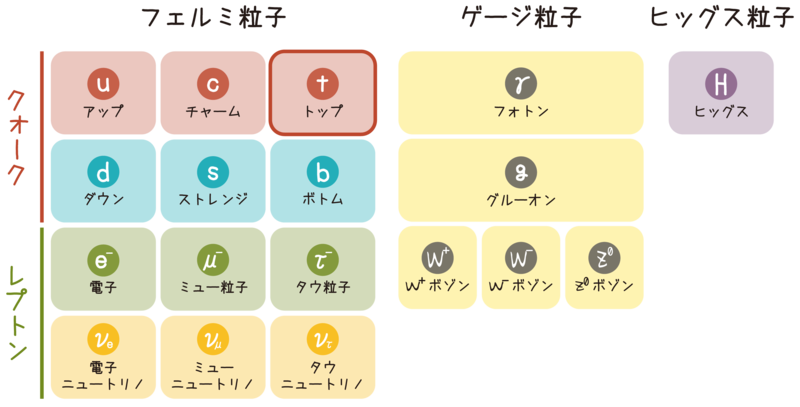
物質をつくる素粒子「フェルミ粒子」や、力を伝える素粒子「ゲージ粒子」、昨年発見されて話題になった質量を与える素粒子「ヒッグス粒子」も仲間に入っています。表にはないですが、各フェルミ粒子の逆の電荷を持つ「対称性粒子」というのもあります。
そして、トップが含まれるフェルミ粒子は、大きく2つに分けられます。「強い力」「弱い力」「電磁気力」「重力」の4つのすべての力がはたらく「クォーク」と、強い力以外の3つの力がはたらく「レプトン」です。
18年越しの快挙!全てのクォークが出そろう!
クォークは20世紀後半から次々と発見され、1988年に5番目のボトムを発見。相方のトップもすぐに見つかるだろうと考えられてきました。しかし、待てど暮らせど見つからない。月日が流れること18年。苦慮の末、1995年にようやく発見されました。現在考えられているモデルにおいて、ようやく
全てのクォークがでそろったのです!
「なぜ私たちが存在するのか」を説明する粒
出そろったらどうなるの?という質問に答えると、壮大な話に突入します。星や私たちなどをつくる物質が、宇宙に生まれたときの話です。
できたばかりの宇宙は、灼熱の超高エネルギー状態。そこから「粒子」と「反粒子」が同じ数だけ生まれました。反粒子は、粒子と回転が逆向きで、電荷の符号が反対の粒子のことです。でも「粒子」と「反粒子」が出会うと、再びエネルギーに戻ってしまいます。生まれては消え、生まれては消え・・・。下の動画のような反応が、あちこちで繰り返されていたと考えられています。

ここで、疑問が浮かびます。
「粒子」と「反粒子」が同じ数だけ生まれて消えるならば、
なぜ「粒子」だけが今残ったの?
粒子と反粒子が同じ数だけ生まれて消えたならば、宇宙には粒子が存在せず、星や私たちも生まれていないはずです。でもこの宇宙には粒子だけが残り、物質があります。一体なぜなのでしょうか?
科学者たちはこう考えました。
「粒子」と「反粒子」は振る舞いが違うのではないか
このことを「CP対称性の破れ」と呼んでいます。そして、クォークが3種類だと考えられていた1973年に、「CP対称性の破れを説明するためには、クォークは少なくとも6種類あるはずだ」と予測した科学者がいるんです。 皆さんも名前を聞いたことがあるであろう日本人。2008年にノーベル物理学賞を受賞した、小林誠教授と益川敏英教授です。
トップの発見は2人の理論を裏付ける証拠になりました。
粒子がなければ、銀河も太陽系も地球も、私たちも存在しません。トップの発見は「私たちはなぜ宇宙にいるのか?」という問いの答えにつながるかもしれません。
ノーベル物理学賞の発表は10月8日(火)の日本時間18時45分ごろです。
2013年ノーベル賞の関連記事
(リンクはすべて削除されました)
2013年ノーベル賞を予想する!
生理学・医学賞その1(by鈴木啓子)
生理学・医学賞その2(by西原)
生理学・医学賞その3(by濱五十鈴)
物理学賞その1(by本田隆行)
物理学賞その2(by福田)
物理学賞その3(by蒋)
化学賞その1(by大渕)
化学賞その2(by田村)
化学賞その3(by髙橋)
投票サイトに寄せられた皆さまの予想
生理学・医学賞その1
生理学・医学賞その2
生理学・医学賞その3
物理学賞その1
物理学賞その2
化学賞その1
化学賞その2







