
未来館にはいろんな科学コミュニケーター(SC)がいるけれど、数学を専門とするSCはおりません!
そんな中、今日は数学好き?を自称するSC二人が専門外ながら、数学談義(お互いの好きな数学ネタをぶつけ合う会)を始めました。
<登場人物紹介>

■ 円周率の日 ―円周率を計算する日―
スズキ:そういえば今日は3月14日ですね。
マツヤ:そうですね、あの日ですね!
スズキ:そう、円周率(π:パイ)の日です!数学の話をするにはもってこいの日ですね。
マツヤ:ですね!
スズキ:円周率、何桁まで覚えています?
マツヤ:えっ、3.1415......5桁までです。スズキさんは?
スズキ:なるほど。私は3.14159265357989までですかね。うろ覚えですが。
マツヤ:さ、さすが...
スズキ:検索してみましょう。3.14159265358979323846...らしいです。あっていませんでしたね。3.1415926535"8979"が正しい円周率でした。天文学のように近似値を使って誤差が大きくなると困るような場合でも円周率はこの15桁まで使うそうなので、ここまで覚えていれば生きていけそうです。
マツヤ:ところでπって、規則性もなく数字が続いていきますよね。こんな数字どうやって求めるんでしょうね?
スズキ:いくつかあると思いますが、マツヤさんならどうやって求めます?
マツヤ:ぼくなら「ビュフォンの針」ですね。確率の考え方で求められます。
スズキ:マツヤさんは数学の「確率」が好きなんですね。「ビュフォンの針」良いですね。どうやって求めましょうか?
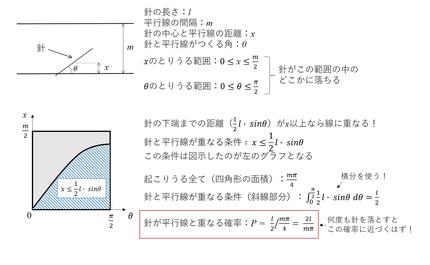
マツヤ:平行線を何本か引いて、そこに針を落とします。このとき、平行線と針が交差するかどうかは、落ちた針と平行線の距離、針と平行線がつくる角度によります。ここから針が交差する確率を求めてみると、平行線の間隔と針の長さ、そしてπを含んだ簡単な式になります(※補遺1参照 )。この確率とπの式を利用してπを求めます。実際にやってみましょう!
マツヤ:1人で爪楊枝(針の代わり)を落とし続けるのはつらいので3人でやりましょう!(SC綾塚を呼び出す)

...50本投げました。
...100本なげました。 ...200本...1000本!
マツヤ:1080本中537本重なったので、そこからπが3.217...(小数点以下第四位より下は無視)と計算されました。うーん、労力のわりにπに近づきませんね。
スズキ:マツヤさんが覚えていた円周率の桁数よりも少ないですね。
マツヤ:もっと簡単に求められないですかね...
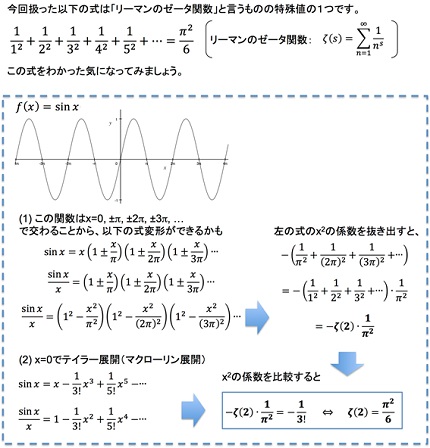
スズキ:そうですね。私が覚えている中で簡単な求め方としては、整数をうまく並べて足し合わせていく方法ですかね。具体的には整数の冪乗(べきじょう)の逆数を無限に足していく方法です。
整数の2乗などの逆数(1/整数の2乗)を計算して足し合わせると、それは円に関する式の一部となり、円周率が含まれる数になるのです(※補遺2参照 )。
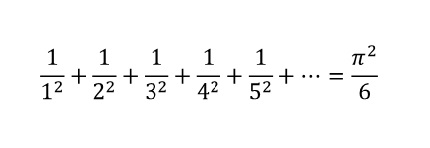
スズキ:せっかくなので手計算してみましょう! 二人で分担して計算しますか。

18の2乗のところまで計算すると、、、3.09...まで何とか計算できました。ビュフォンの針の計算結果よりは若干良いですね。
マツヤ:でも、πに近づく速度、いまいちですね。
スズキ:わかりました。じゃあ、もうちょっと改造したものを使ってみましょう。
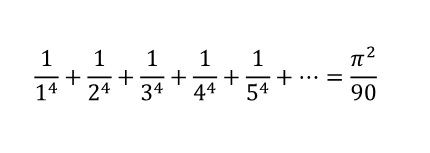
18まで(Excelが)計算すると3.141554506になりますね。
マツヤ:おお!
スズキ:せっかくなんで100まで(Excelで)やってみましょう。3.141592415。3.141592まであってますね。
マツヤ:7桁まで行けましたね。
スズキ:これでも、さっき検索した15桁までは遠そうですね。
マツヤ:道のりは長いですね...
スズキ:じゃあ、私が知りうる限り一番高速にπに近づく式、「ラマヌジャンの式」 を使いましょう! ラマヌジャンはインドの数学者でして、天才的な洞察力で様々な関係式や法則を発見した人です。しかし、自身の発見の証明を残しておらず、後世の人が証明しているんです。この式もそんなラマヌジャンの式の1つです。

k=0~1、3.14159265358979(※ これ以上はExcelの表示可能桁数の都合上、簡単には出せませんでした)
マツヤ:あ、あっという間に、パソコンの計算精度を超えましたね!
―――
――
―
■ さて、どんな数学トピックが好みか
スズキ:ここまでやってみたところ、円周率を求めるには、確率はそんなに良い手法ではなさそうですが、マツヤさんは確率のどんなところを気に入ってるんですか?
マツヤ:確率の考え方は日常生活でも役に立つところですね。
スズキ:日常?どんなシーンですか?
マツヤ:日常生活にはいろいろな確率があると思うんですけど、 例えば、ある検査を受ければ90%の確率で病気であるとわかる、こんな検査があったとします。もしスズキさんがこの検査を受けて、陽性が出たとします。この時、スズキさんが病気である確率はどれくらいだと思いますか?
スズキ:実際にその病気にかかっている人が、その病気かどうかわかる検査をしたとき、90%の確率で陽性が出るということですね?逆にいうと、その病気なのに、陰性(病気でない)の結果が出てしまうことが10%。本当は病気ではないのに、陽性となってしまう場合(偽陽性と呼ばれる)もありそうだし......今出てきた数字だけじゃわからないですよね?
マツヤ:そうですね。そもそもこの病気にかかっている人がスズキさんと同じ年代・性別で世の中で0.8%いるとします。あと陽性が出る確率が必要で、ここでは8%としましょう(真の陽性と偽陽性を合わせた数字)。ベイズの公式を用いると、スズキさんがもし陽性判定されたとしても、本当に病気である確率はたった9%と計算されます(※補遺3参照 )。
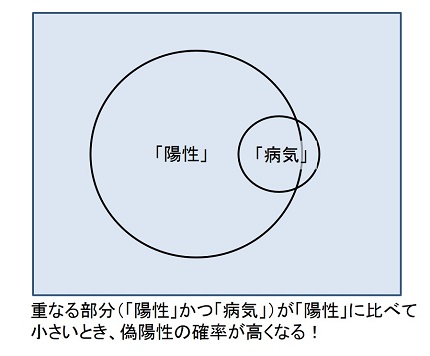
スズキ:おお~ 陽性判定の精度が高い検査で陽性が出ているのに、案外病気である可能性は低いんですね。では、もう一度私が検査したとして、もう一度陽性が出たら、本当に病気である可能性はどのくらいなんですか?
マツヤ:2回続けて陽性判定となった場合には、病気である確率が54%まで上がります。
スズキ:やっぱり検査は繰り返したほうがより正確な結果が出るわけですね。
マツヤ:そうですね。複数回受けて判断するほうが良いですね。
マツヤ:私は確率が好きなのですが、スズキさんはどんな数学のどんなところを気にいっているんですか?
スズキ:私は数学の中で特に整数、いわゆる普通の数字についての数学が好きです。例えば、整数の四則演算、つまり足し算・引き算・掛け算・割り算は簡単にできるじゃないですか。 でも、その整数の四則演算の中にもまだわかっていないことがあるんです。
マツヤ:え?わかってないことなんてあるんですか?
スズキ:いろいろありますよ。
例えば、好きな正の整数を1つ思い浮かべてください。2桁くらいの方がマツヤさんの負担が少ないと思います。あ、その数字は言わなくていいですよ。
マツヤ:はい、思い浮かべました。
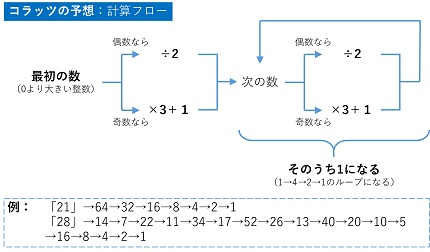
スズキ:では、その数字が偶数だったら2で割ってください。奇数だったら3倍して1を足してください。
マツヤ:はい。
スズキ:では、新しくできたその数字も、偶数だったら2で割り、奇数だったら3倍して1を足してください。以下、この操作を繰り返します。そうすると、最後は1になります。
どうなりました?
マツヤ:はい、何度かやったら1になりました!
スズキ:やはりそうでしたか! ちなみに最初の数字は何を選びました?
マツヤ:最初、21を選びました。
スズキ:ほかの数字でもきっと最後は1になりますよ。 試してみてください。
これは「コラッツの予想」と呼ばれていて、どんな正の整数を選んだとしても最後は1が出てくると予想されています。ただ、証明されておらず、未解決の問題です。
マツヤ:こんな単純な問題なのに、未解決とはびっくりですね。 でも、当たり前というか、そんなに不思議な感じはしませんね。
スズキ:なるほど。 では試しに「27」でさっきの操作を試してみてください。
マツヤ:1になるはずですね、やってみます!
スズキさん、ぜんぜん小さくなりません。いま161です...
スズキ:そうでしょう! 27を選んだ場合はなかなか小さくならず、一度、9232まで大きくなります。 ただ、最後はちゃんと1になります。こんなふうに、理解しやすくて簡単な話なのに、分かっていない、証明されていないというのが面白くて好きです。
マツヤ:確かに、意外性もあって面白いですね。
―――
――
―
■ それぞれの数学観
マツヤ:こういった整数の話は、なにか社会で役立ったりするんですか?
スズキ:整数そのものは社会でも使われています。
でも、役立つかどうかよりも、整数という普段使っている普通の数字なのに、円周率が出てきたり、未解決の問題があったりという話が「面白い」ということを言いたかったんです。
マツヤ:はい、面白さは伝わってきましたよ。でも、確率の話は、面白いうえに、日常生活にもかかわるので、僕としてはやっぱり確率の方が魅力的ですね。それに、たとえば迷惑メールのフィルタリングなんかに確率論は応用されていて、社会でも役立っています。
スズキ:数学が社会に応用されるのは、その理論が見つかってからずっと後です。たとえば、2017年のノーベル物理学賞の重力波は100年前にアインシュタインが予想していますが、アインシュタインがその予想に利用した数学はリーマンがさらに約60年前に確立しています。その160年前のような、まだ何の役に立つかわからないけどとりあえず面白いから研究してみた、という状態が面白いんです。
マツヤ:そこに異論はないんですけど、物理学は宇宙やら自然現象を解き明かす学問ですし、確率論も自然や社会の事象を対象にできます。ですので、自然科学と言えますよね?整数論はどうなんでしょう?
スズキ:整数論というか数学は、数そのものを追求するもの。自然科学以前の、宇宙を越えて常にある本質を解き明かすものだと思っています。整数論はそのことをわかりやすく直接的に見せてくれます。自然科学のどこで役立つかなんてというのはまた別の話です!
マツヤ:そうですか...
スズキ:はい!解散!!
以下補遺
補遺1.ビュフォンの針
補遺2.ゼータ関数(バーゼル問題)
補遺3.ベイズの公式

備考
スズキ(鈴木毅)過去記事一覧





