
こんにちは!
山内からバトン (リンクは削除されました)を受け継ぎました、科学コミュニケーターの坪井です。
今回は2016年ノーベル物理学賞の3本柱の中の1つ、ホールデン博士が1983年に発表したホールデン予想(Haldane's conjecture)のお話です。
前回は「2次元にある小さな棒磁石の渦がペアになったり離れたりすることで相転移が起こる」という話でした。今回の主役も小さな棒磁石たちですが、舞台は2次元ではありません。
なんと!
い ち じ げ ん !!!
1次元にある小さな棒磁石たちが、ビックリするようなことを引き起こします。
さあ、順に見ていきましょう!
本日のお話の流れ
- 舞台は1次元で、主役はスピン
- 素直に揃うか、天邪鬼に揃うか
- 1次元でのスピン
- スピンの大きさ
- 1/2より大きなスピンのふるまい
- すぐには受け入れられなかったHaldaneの発見
舞台は1次元で、主役はスピン
まず、お話の舞台と主役を確認しましょう!
冒頭でもお話ししたとおり、舞台は1次元!! 線の世界です。
ホールデン博士は、数式を解いてその世界を調べました。
実際の物質でも原子がくさり状に並んだものを擬似1次元として考えることができます。

主役は、前回と同じく小さな棒磁石たちです。
原子のくさりのどこにいるかというと...
いたいた!
原子の中にいる電子が、小さな棒磁石の正体です。
小さな棒磁石は、原子核の周りの軌道の上にいます。それぞれの軌道には、下の絵のように、専用の部屋が用意されているのです。
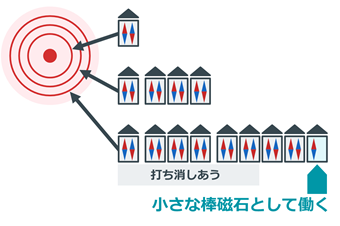
1つの部屋に入れるのは2つまでです。
2つ入るときは逆向きになり、お互いの磁石の性質を打ち消し合います。つまり、満室の部屋は磁石の性質を示さなくなります。そのため、1つの原子の磁石の性質を見るためには、ペアになっていない棒磁石(不対電子)だけを考えれば大丈夫です。
つまり、原子のくさりは、ペアになっていない棒磁石だけ考えてこのように表すことができます。
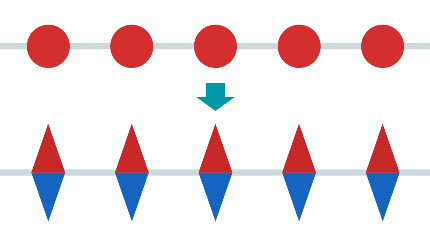
これが今回の舞台「一次元」にいる、主役の「小さな棒磁石」たちです。
ここからは少しレベルを上げて、小さな棒磁石のことを「スピン」と専門用語で呼びます。
なになに?急に難しくなりそう?
いえいえ、大丈夫!
そんなこともあろうかと、ぶつりーずの得意技をご用意しました。
いけぇえええーーーーー、擬人化ぁあああ!!!!
と、いうわけで、
科学コミュニケーターの仲間たちにスピンになってもらいましょう。

あらびっくり。
スピンがとっても親しみやすくなりましたね!
ここからは、登場する科学コミュニケーターすべてをスピンとお読み替えください。
素直に揃うか、天邪鬼に揃うか
まず、復習がてら3次元の物質の中のスピンを見てみましょう。
前回の記事にあったように、温度が高いとき、スピンの向きはバラバラになりますが、温度が低いとスピンは揃います。
どうして揃うかというと...
スピンは科学コミュニケーターと同じでおしゃべりが大好きだから。特に温度が低いと隣のスピンとよくおしゃべりをして、「私もそっち向く!」と同じ向きに揃います。この状態が一番心地良いようです。
身の回りにある磁石の中は、下の図のようにスピンが同じ向きに素直に揃っている状態です。

物質によっては、違う揃い方もあります。
隣のスピンと逆さを向く天邪鬼な揃い方です。温度が高いとバラバラになるのは素直に揃うスピンたちと同じですが、温度が低いときには隣の人と逆を向くのが「心地いい」状態になります。
隣同士で「ちょっとあっち向いてよ!」とおしゃべりするんですね。

心地いいのが、素直な揃い方なのか、天邪鬼な揃い方なのか※1は、スピンを持っている原子同士のつながり方によって決まります。
素直に揃ったスピンを持つ物質を「強磁性体」、天邪鬼に揃ったスピンを持つ物質を「反強磁性体」と言います。
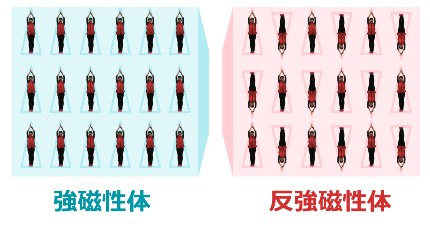
1次元でのスピン
では、1次元で低い温度のとき、スピンはどうなると思いますか?
厳密には、1次元のスピンは揃いません。しかし、揃わないとしても「スピンにとってどのような状態が一番心地よいのか」を考えることは、理論物理では重要なのです。
一番心地よい状態は、直感で考えるとこれに近そうですよね?
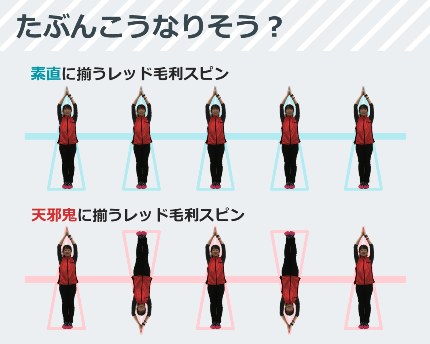
実際はどうなのか、量子力学を使って計算すると...
素直に揃っていたスピンたちは、量子力学の下でも直感通りに隣と同じ向きに揃うとわかった一方で、天邪鬼に揃っていたスピンたちに量子力学の計算を適用すると1次元では「どこも向かない」という謎の計算結果に...!
直感では理解できない状態になっていることがわかりました。とことん天邪鬼ですね。
この天邪鬼に揃うスピンたちの1次元での状態を調べたのは、物理学者 ハンス・ベーテ博士で、1931年のことでした(ベーテ仮設)。

この状態に少しずつエネルギーを加えてみます。
まず、素直に揃う強磁性体のスピンたち。
一番心地よい同じ向きに揃った状態から、もらったエネルギーを使ってスピンは隣と少しずつずれていきます。エネルギーをもらったスピンは、ちょっとずつ自己主張が強くなるイメージです。

次に、天邪鬼に揃う反強磁性体のスピンたち。
最初の状態は、本当は絵では描けないような状態ですが、ここでは説明のため隣と逆さを向くように描いています。
エネルギーを加えると、素直に揃うスピンと同じように、もらったエネルギーを使ってスピンは少しずつずれていきます。
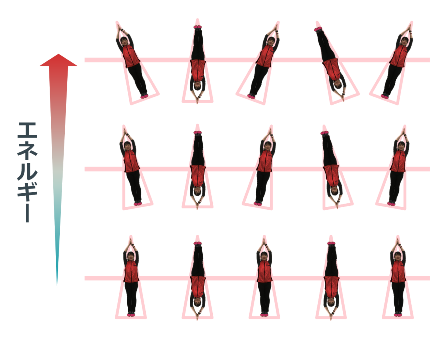
以上が、ホールデン予想の前までにわかっていたことです。
スピンの大きさ
さて、ここまではレッド毛利スピンが活躍しましたが、科学コミュニケーターにもいろんな身長の人がいるように、実はスピンにもいろんな大きさがあります。
スピンの正体は、上向きと下向きのペアでない電子だとお話ししましたが、ペアでない複数の電子は、まとめて1つの棒磁石とみなします。そして、電子の数が増えた分の大きさが大きくなります。
実際の物質では、元素の種類によって電子の数も変わるので、ペアでない電子の数も変わります。つまり、スピンの大きさは元素によって変わります。
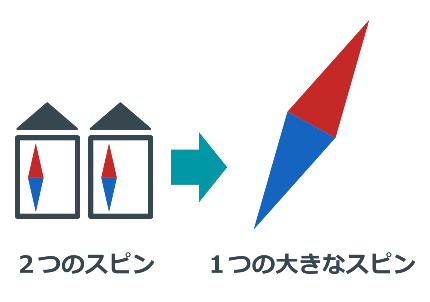
スピンの大きさは、電子が1つのとき、1/2と決まっています。
なので、
2つだと 1/2+1/2=1
3つだと 1/2+1/2+1/2=3/2 ...
と1/2ずつ増えていきます。
とびとびの値をとるところは、人間の身長と違いますね。
なので、無理やりとびとびにしました。うふ♡

ホールデンが見つけた摩訶不思議なふるまい
いよいよ、ホールデン予想の中身に入っていきます。
大きさが1/2の素直に揃うスピンたちと同じく大きさが1/2の天邪鬼に揃うスピンたちについて、低温のときの状態とエネルギーが与えられたときにどうなるかは、すでに明らかにされていました。
では、1/2よりも大きなスピンは、低温のときどのような状態になると思いますか?
そこにエネルギーを与えて行ったら、どのように変化すると思いますか?
「いやいや、大きさ変わったって同じでしょ?」
と、思うのではないでしょうか?
ベーテによって天邪鬼に揃うスピンのふるまいがわかった後、50年以上もの間、多くの物理学者もそう思っていました。
その「無条件に信じられていた常識」を疑い、トポロジーを使って天邪鬼に揃うスピンの新しいふるまいを見つけたのが、今年のノーベル物理学賞を受賞したうちの一人、ホールデン博士だったのです。
ホールデン博士が見つけた、天邪鬼に揃うスピンの新しいふるまいとは何でしょうか?
それは
「天邪鬼に揃うスピンたちの1次元での性質は、スピンの大きさが整数か半整数かによって全く異なる!」
というものです!!
これは、本当に信じがたいことです。
どれくらい信じがたいのか、水で例えて考えてみましょう。
現実にはありませんが、もし、大きさが1/2, 1, 3/2, 2...の水分子があったとしたら...
「水分子の大きさが整数か半整数かによって、凍ったり溶けたりなどの水のふるまいが変わる」ということが起こってしまうようなものです!
水分子の大きさが違うだけで、構成する原子も分子同士の関係性も変わらないのに...!
摩訶不思議ですよね?
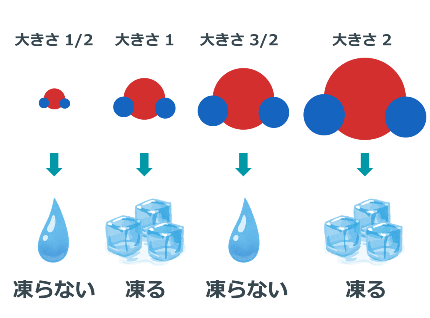
1/2より大きなスピンのふるまい
では、そんな摩訶不思議な現象が起きているとき、スピンたちはどうなっているのか見てみましょう。
大きさが1であるオレンジ片平スピンの、素直な揃い方と天邪鬼な揃い方を比較してみます。
まず、素直な揃い方(強磁性体)。
一番心地よい状態は同じ方向に揃った状態で、エネルギーを少しずつ加えるとその状態から、少しずつずれていきます。大きさ1/2の素直な揃い方と全く同じですね。
さらに、大きさ1、3/2...とより大きなスピンになっても、全く同じふるまいをします。
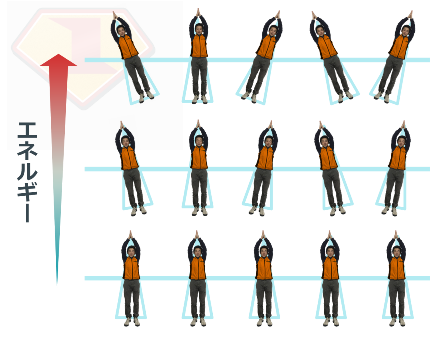
次に、天邪鬼な揃い方(反強磁性体)。
天邪鬼に揃う大きさ1/2のレッド毛利スピンと同じく、大きさ1のオレンジ片平スピンも最初の状態が絵では描けないような状態をとるのですが、スピンの揃い具合がちょっと変わります。隣の向きを気にせず、より自由気ままな向きを向きます。
(ここでは、この後の説明のため、無理やり隣と逆向きに揃った絵として表すことにします。)

次に、オレンジ片平スピンにエネルギーを加えてみましょう。

あれ? 変わっていません...!
もっと加えるとどうでしょうか? えい!えい!

おお!やっとオレンジ片平スピンが、エネルギーを得てさらにずれ始めました。この後は、同様にエネルギーを加えるほどずれていきます。
このように、状態が変わるために超えなければならないエネルギーの溝があることを「エネルギーギャップがある」といいます。

同じ天邪鬼に揃うスピンでも、大きさ1/2のレッド毛利スピンとは違い、大きさ1のオレンジ片平スピンにはエネルギーギャップがあることがわかったのです!!(驚きポイント その①)
これは、誰も想像していなかった結果でした。
もっと面白いのはここからです。
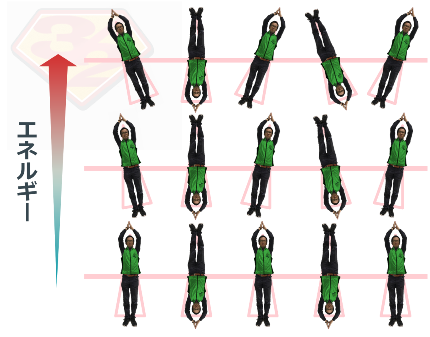
天邪鬼に揃う大きさ3/2のグリーン田代スピンはどうなると思いますか?
な、な、なんと!
エネルギーギャップがなく、エネルギーを加えた分だけスピンが少しずつずれていきます!
天の邪鬼に揃う大きさ1/2のレッド毛利スピンと同じふるまいです!
では、さらに大きな大きさ2のブルー宗像スピンは??
な、な、な、な、なんとぉおおおーーーーー!
また、エネルギーギャップが現れたーー!!!

このように、スピンの大きさが、1/2, 3/2などの半整数か、1,2などの整数かによって、その相の性質が全く異なることをホールデン博士が理論的な計算から
示したのです...!!(驚きポイント その②)
エネルギーギャップがあるということは、ある一定以上のまとまったエネルギーを与えてもらわないとそれを受け取れないということなのです。
例えばエネルギーギャップがある状態に磁場を加えてスピンを動かそうとしたとき、徐々に変わるのではなく、あるときを境に、不連続にガラッと変わります。つまり、「相転移」が起きているということなのです。
すぐには受け入れられなかったHaldaneの発見
トポロジーの考え方が生かした理論的な検証計算から、このような摩訶不思議な物質のふるまいを見つけたホールデン博士。
あまりに信じがたい結果だったゆえ、発表後も簡単には受け入れられなかったそうです。
(論文が難解すぎて同分野の専門家が読んでもわからないほどというエピソードも。)
そのような経緯から、この発見には「ホールデン予想」という名前がつきました。
理論物理は理論なので「予想」なのは当たり前なのですが、わざわざ「予想」をつけるほど、他の物理学者に信じられなかったのです。
そうして、この予想に多くの物理学者が興味をもち、より詳しい計算や実際の物質での実験、さらにはコンピューターを使った計算などによって、ホールデン予想は複数の裏付けを得られるようになり、やっと受け入れられるようになりました。
誰も知らない世界を切り拓いているわけだから、それが正解か間違いかなんて、その時点では誰もわからなくて当たり前。その後に続く科学技術の発展により、やっと「確からしい」と分かってくるのです。
科学者は、まさに人類の地のフロンティアを切り拓いているのですね。
***
このホールデン予想の大枠を理解するまで、私は1か月かかりました。
その1か月は、少しずつわかることが積み上がっていく、とても愉しい時間でした。
中でも一番感動したのが、この発見のすごさが自分の感覚で「わかった」とき。
「こんなにすごい発見を人類で初めて『わかった』ホールデン博士は、その瞬間どんな気持ちになったんだろう?」
そう思うと、感慨無量でした。
「わかりたい!」というノーベル賞発表直後の気持ちを書いたブログ (リンクは削除されました)でお約束した通り、できる限り皆さんにも「わかった!」と言っていただけるよう、この発見のすごさが伝わるよう魂込めて書きましたが、どうでしょうか?
今年のノーベル物理学賞について、少しでも新しいことを知ったり、なんとなくでも「すごそう」と思ったりするきっかけにこの記事がなったなら、この上ない喜びです。
ぶつりーずのブログリレーも、いよいよ次回が最終回。
我らがぶつりーずリーダー、雨宮の登場です。
次回もどうぞお楽しみに!

「わかった」への相転移
①ブログリレーでもう一度解説します (リンクは削除されました)
②2次元での相転移を説明したKT転移 (リンクは削除されました)
③1次元ではもっとすごい相転移が起こる (この記事)
④量子ホール効果をトポロジー (リンクは削除されました)
参考文献
このブログの執筆にあたって、多大な協力をいただいた未来館の47期ボランティアでもある中島多朗さん(理研・創発物性科学研究センター)からご紹介いただきました。
● 勝又紘一・田崎晴明 責任編集 「物理学論文選集 VIII : Haldane Gap - スピン系におけるマクロな量子現象」日本物理学会 1997年
● 久保健・田中秀数 著 「朝倉物性物理シリーズ7 - 磁性I」朝倉書店 2008年
※1 磁性体のふるまいを決める式(ノーベル財団のAdvanced Information内の式(1))における交換相互作用 Jが正の値をとるスピン系を「素直に揃うスピンたち」、Jが負の値をとるスピン系を「天邪鬼に揃うスピンたち」と表現しています。







