こんにちは！ぶつりーず最年少（のはず）の山内です！
お待たせしました、ノーベル物理学賞 ブログリレー第2弾！
今回から、本格的に受賞内容について紹介していきます。
みなさま、焦らず急がず、じっくりと行きましょう...！

今回の内容は、コスタリッツ博士とサウレス博士によって理論的に発見された「KT転移」と呼ばれる現象についてです。
いきなり難しい単語が出てきましたが、ご安心ください。 「KT転移」は、お二人の名前（Kosterlitz博士、Thouless博士）の頭文字から名付けられているだけです。
むしろ、名前の頭文字で表されるほど、重大な発見だったのですね。

...でも正直に告白します。
今回の話、やっぱり難しいです。

いや、言い直しましょう。難しくない研究など、この世に存在しないのです。
研究者は、誰も目をつけていなかった分野を見つけ、開拓すべく苦難を乗り越えながら進んでいます。
その中でも、紙とペンと数式と頭脳だけで切り開いてゆく「理論物理」が、今回のおはなし。
難しくないワケがないのです。

しかし、しかしです。
苦しみにも耐えて登り切るからこそ、山頂から見る景色は荘厳な絶景となるのです。
その絶景を我が眼で見たいからこそ、人は山へと挑むのです。

今回は、私山内が案内人として最後までお付き合いします。
「わかった！山」の山頂から見える絶景を目指し、一緒に歩みましょう！
ぜひ、最後までついてきてくださいね！！！

まずは、ウォーミングアップ

登山をするためには、まずウォーミングアップが必要です。
前回の坪井の記事で「トポロジー」「相と相転移」について簡単に紹介しました。
ここでは、非常に重要な「相と相転移」の復習をしつつ、今回の舞台の確認をします。

☆「相」「相転移」のおはなし

たとえば私たちに身近な水は、温度によって氷や水蒸気に変わります。
この、氷［固体］・水［液体］・水蒸気［気体］の状態にあることを「相」と呼び、この相の間を移り変わることを「相転移」と呼びます。

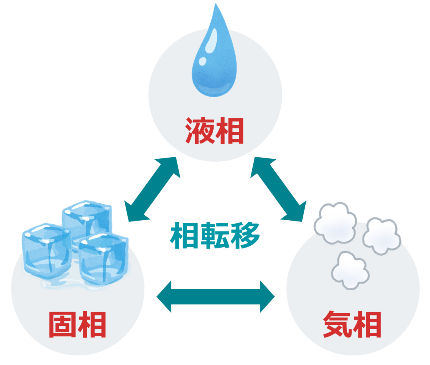
この意外と身近な「相と相転移」、実は水だけで起こるわけではありません。

磁石にも、同じような相と相転移があるのです！

磁石の相転移は、「磁石の状態」から「磁石ではない状態」へと移り変わります。
例えば、地上最強の永久磁石「ネオジム磁石」だと、310℃くらいまで加熱すれば磁石の性質を失い、なんにもくっつかなくなります。

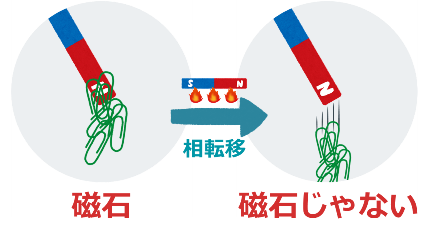
このように、物質の「磁石の性質を持つ状態」または「磁石の性質を持たない状態」をそれぞれ「相」として、これらの状態が移り変わることを「相転移」と考えることができます。
今回のおはなしでの「相転移」は、こちらのことを指しているんですね。

しかし、皆さん。ここで一つ気になりませんか？

「なんで同じ物質なのに磁石になったりならなかったりするんだろう」と。

...そう、この疑問が今回のおはなしのキーポイントなのです！

実は、物質の中身をものすごく拡大して（分子や原子のスケールで）見てみると、小さな棒磁石が集まってできています。

（正確には、磁石に含まれる鉄やニッケルといった原子一粒一粒が棒磁石にあたり、「磁気モーメント」または「スピン」と呼びます。）

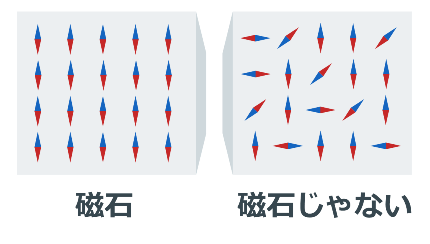
この小さな棒磁石がそれぞれバラバラの方向を向いているとき、物質は磁石の性質を持ちません。
しかし、小さな棒磁石がすべて同じ方向に揃うと、物質は磁石になります。

（専門用語で、前者を常磁性、後者を強磁性と呼びます。）

ここで、磁石に温度を加えてみると...？
綺麗に揃っていた小さな棒磁石が、ある温度を境に突然バラバラの状態へと移り変わります！
これが磁石における相転移の正体で、「磁気相転移」と呼びます。

（専門用語で、相転移が起こるある温度のことを転移点と呼びます。）

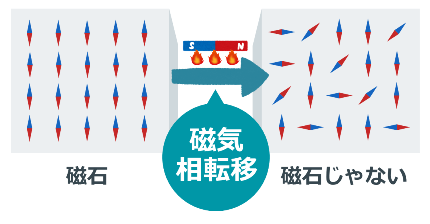
この「磁気相転移」が、今回のおはなしのスタートライン。
ここから、コスタリッツ博士とサウレス博士が発見した「KT転移」の本題へと入っていきます。
みなさま、お待たせしました。「わかった山」への登山の始まりです！

"2次元"が、今回のおはなしの舞台

ここまでの「磁気相転移」のおはなしは、すべて「3次元の世界」であることが大前提でした。
私たちの世界は、縦・横・高さの3つの軸がある「3次元」です。先ほどの磁気相転移も、3次元の世界で当たり前に起こっている現象でした。

ところが、1つ軸を減らした「2次元平面」の世界では、話が全く異なります。
なんと、3次元の当たり前が起こらないのです！

...2次元といっても、画面の向こう側のアニメの世界じゃないですよ？

残念。

今回の「2次元」とは、磁石の表面をものすごーーくうすーーーーーく切ったものだと思ってください。
本当に磁石をうすーーーく切るのはとても難しいですが、ここは紙とペンと頭脳の世界"理論物理"。想像するのに、不可能はありません！
コスタリッツ博士とサウレス博士は、理論的なモデルとして2次元を仮定したのです。

（後に行われた実験では、だいたい原子1個分くらいの薄さで擬似的に2次元の世界を創り出しています。）

この2次元平面の上に、先ほど紹介した小さな棒磁石が敷き詰められている状態が、今回のおはなしの舞台です。

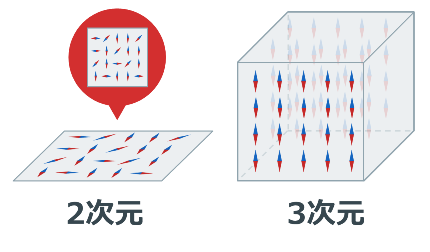
さて、この2次元の世界では、3次元の世界とはいろいろ違ったことが出てきます。
特に注目したいのが、小さな棒磁石の向きです。

「棒磁石の向きが全部揃うと磁石になる」と先に紹介しましたが、これは3次元での話。2次元だと、棒磁石の向きが「全部同じ方向に揃うことは無い」ことがわかっていました。
つまり、「磁気相転移」は2次元の世界では起こらないと思われていたのです！

これはマーミン・ワグナーの定理と呼ばれていて、厳密な計算から見つかったものでした。
正確に説明するのは至難の業ですが、乱暴に説明すると以下のようになります。寄り道になるので、気になる方以外は読み飛ばしてもOKです。

---

2次元で小さな棒磁石が揃わないのは、「自分の周りにいる仲間（棒磁石）が少ないために、棒磁石の方向が大きく揺らいでしまう」ために起こります。3次元だと上下前後左右（の3軸上）に仲間がいますが、2次元だと前後左右（の2軸）しか仲間がいません。
仲間の少ない2次元で、しかも棒磁石がある程度自由に回転できる今の舞台では、どうしても揺らぎを抑えきれず、全員が同じ方向を向いてくれないのです。

---

やっぱりややこしいので、「マーミン・ワグナーの定理から、棒磁石が全部同じ方向に揃うことは無い」ことだけ覚えておいてもらえたらバッチリです！

めちゃくちゃ低温にしても...

「揃わぬなら、揃えてしまえ、棒磁石」
ではありませんが、実は棒磁石を揃えやすくする方法があるんです。
その方法が、「冷やす」ことです。

そもそも、小さな棒磁石は温めることでバラバラな方向を向き始めました。
逆に考えれば、温度の低い状態では向きが揃っているはず。
実際、温度が低ければ低いほど、小さな棒磁石はどんどん揃いやすくなります。

...と言うことは、ものすごく冷やせば2次元でも揃うかもしれない？！
と思われた方、とても鋭い！

結論から言うと、絶対零度に近い－270℃くらいまでものすごーーーーく冷やしても、残念ながら完全には揃いません。
しかし、温度が低い分、棒磁石は「とても揃いたい」状態となります。
その結果、「ほとんど棒磁石が揃っているのに、完全には揃いきれない状態」が生まれます。

揃いたいのに揃えない。棒磁石にとっては、なかなかもどかしい状態でしょうね...
いやーとても不思議な現象だ...

しかも、よくよく考えたら「揃いたいけど揃いきれない状態」から「バラバラの状態」も、大きく変わっているんですよね...
不思議なことだらけだ...

......もうお気づきになったでしょうか。
そう、コスタリッツ博士とサウレス博士は、これらの「不思議」を解き明かしたのです！

実はあった！相転移！

さて、今回の「わかった！山」もついに8合目。ここからが一番楽しいところ！
ついに、コスタリッツ博士とサウレス博士が登場します！
...でもその前に、少しだけ整理をしましょう。

---

まず、お話の舞台は「2次元の物質（磁性体）」です。その中をずーーっと拡大すると、小さな棒磁石が敷き詰められています。
温度を極低温にしたとき「棒磁石が揃いたいけど完全には揃わない状態（相）」になっていて、そこから温めていくとある温度を境に「バラバラの方向を向いた状態（相）」に転移します。
そこで、まず「揃いたいけど揃わない状態」を明らかにして、そこからどうやって「バラバラの方向を"向きはじめた"状態」に転移するか、その境目に注目して考えていきましょう！

---

コスタリッツ博士とサウレス博士は、「揃いたいけど揃わない状態」を明瞭に解き明かしました。
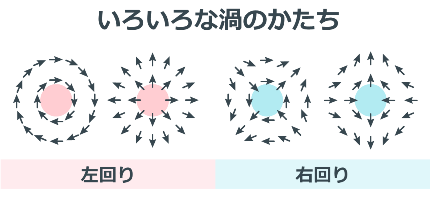
なんと、これは小さな棒磁石が「渦」状に並んでいる状態である、というのです！

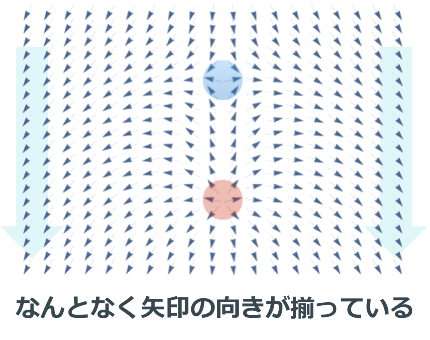
上図が、その「渦」状に並んでいる様子です。矢印の方向が小さな棒磁石の方向を表しています。また、赤と青の丸印が渦の部分です。

ぜひ、よーーーーーく見てみてください。
確かに、渦の周辺は矢印がバラバラの方向を向いています。でも、図の右端と左端は何となく同じ方向を向いているように見えませんか...！！
そう、これが「揃いたいけど、完全には揃わない状態」の正体なのです！！！

そして、とても重要なポイントが1つあります。
それは、「右回りと左回りの渦がペアとなっていること」です。
実は、先ほどの図の赤丸は左回りの、青丸は右回りの渦を表していました、

（正確には、渦と反渦です。詳細は後述します。）

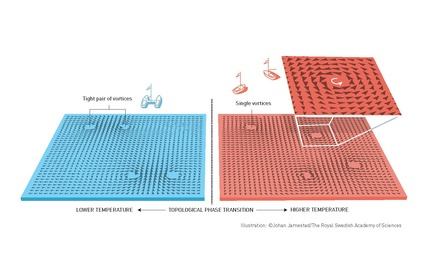
渦がペアを組まず、1つだけだったり、離ればなれになったりすると下図のようになります。

これだと、渦の周りだけではなく、図の端の方も含めたすべての矢印がバラバラの方向を向いてしまっています。
あれ？「矢印がバラバラ」...聞き覚えが...
...そう！これこそが、「バラバラの方向を向いた状態」であり、ある温度超えて相転移したときに起こることなのです！！

つまり、「揃いたいけど揃わない状態」から「バラバラの方向を向いた状態」への転移は、2種類の渦がペアになっているか、離ればなれになっているかというふるまいによって起こることがわかったのです！！！

このように、コスタリッツ博士とサウレス博士は、「小さな棒磁石がすべて同じ方向を向くことはない」というマーミン・ワグナーの定理を守りつつも、「揃いたいけど揃わない状態」から「バラバラの方向を向きたい状態」の相転移を、渦の存在に注目して解き明かしました。
これこそが、今回のおはなしのゴールである「KT転移」なのです！！！！！！！！！！

やりました！！やりましたよ！！！！「わかった！山」登頂成功です！！！！
やったぞ！！！！！！！うわーーーい！！！！

あれ、トポロジーのおはなしは？

.........はい。すいません。登頂成功は嘘でした。
まだ、トポロジーのおはなしをしていませんでした。
ということで、「真の登頂成功」を目指して、もう少しお付き合いください。

ここで、トポロジーについて思い出してみましょう。

『モノを連続に変えた時に、変わらない性質に着目する数学の手法』

これが、前記事で紹介したトポロジーの本質的な意味でした。
では、今回のKT転移においてどこが「変わらない性質」だったのか。

その答えは、「渦」です。

先ほど、渦が右回りと左回りのペアになっているのが大事、と紹介しました。
実は、この渦の右回りと左回りがトポロジーな性質を持つのですが、実はそんなに難しい話ではありません。実際に手を動かしてみると、すぐにわかります！
さあ！みなさん！紙とペンを用意しましょう！

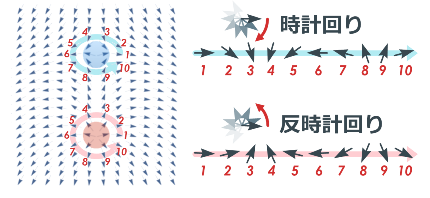
まず、先ほどの赤丸・青丸の周りの矢印を、反時計回りにぐるっと1周分取り出して並べてみます。
すると、どうでしょうか。赤丸の方は、取り出した方向と同じ反時計回りに矢印がちょうど1回転していますよね。
一方、青丸の方は、取り出した方向と逆向きの時計回りに矢印がちょうど1回転しています。

実はこの「矢印が"ちょうど"1回転した」ことがとても重要なのです。
矢印がどの方向を向いていても、もしくは並び方がどれだけ歪んでいても、取り出して「1回転」していればそこに渦があることを示しています。

しかもこの渦、今回の舞台である「揃いたい状態」の中ではどうやっても取り除くことができません。

例えば、私たちの頭にある"つむじ"を思い浮かべてください。
"つむじ"も、髪の毛の方向が1回転している「渦」です。
髪の毛の方向を変えるだけ（抜いちゃダメ！）で、"つむじ"を取り除いてみましょう。

つむじの周りの髪の毛を、ゆっくりと顔の方向に揃えてみて...
あれ、つむじを消したと思っても、新たなつむじがその後ろにできてしまう！繰り返すとどんどん頭の後ろ側に移動してしまう...！？

そうなんです。渦を取り除こうと矢印をなるべく揃えながら動かしても、渦の中心が移動するだけで取り除くことができません。「端」まで渦を移動させたり半分に切ってしまわないと、渦を取り除くことができないのです！

このように、矢印の渦は「特別」なことをしなければ取り除くことができません。すなわち、渦の中心は、決してほどく事が出来ない「穴」が空いていることになります。

そう、「矢印がちょうど1回転することで生まれる渦という穴」こそ、「変わらない性質＝トポロジー」なのです！
そのため、この渦は"トポロジカルな欠陥"と呼ばれており、渦のふるまいによって相転移が起こるので「トポロジカル相転移」と呼ばれています。

（正確には、渦に限らずトポロジカルな欠陥のふるまいで相転移が起こるものをトポロジカル相転移と呼んでいます。）

ちなみに、このトポロジーな渦は、左回り（赤丸）を「+1（正）」、右回り（青丸）を「－1（負）」と整数で表せます（"1"は1回転の意味です）。
この数字をトポロジカルチャージと呼び、「+1」と「－1」で打ち消し合う状態を「渦がペアになる」として考えることで、数式で表せるようにしています。

この「トポロジーで考える」視点を物理学に持ち込むこと自体、非常に画期的なアイデアでした。だからこそ、高い評価を得たのです。

...ということで、みなさま。おめでとうございます！！！！！
今度こそ、「わかった！山」真の登頂に成功です！！！！
いかがでしょうか？ どんな景色が見えますか？
絶景でしょうか？はたまた雲の中でしょうか？
もっと高い山が見えてしまった！なんて方もいらっしゃるかもしれません。
でも、これこそが、研究者のみなさんが見てきた景色なのだと思うと、わくわくしてきますよね。
楽しんでいただけたなら、案内人としてこれ以上のことはありません。

実は磁石だけの話ではなかった！？

さて、あとは下山を残すのみ。
最後に、このKT転移の本当の姿を少し紹介して終わりにしようと思います。

今回、KT転移が「磁石になりうる物質（磁性体）」で起こることを前提に紹介しました。
しかし、それは木を見て森を見ず。
実は、もっともっと多くの場合でも成立するのです。

例えば、ヘリウムの超流動や超伝導体の薄膜、2次元物質の溶解などなど。
2次元をはじめとした「次元の低い」シチュエーションの多くで、このKT転移（の考え方）を使うことが出来ます。
より多くの研究者から必要とされ、KT転移自体もさらに研究がなされ、私たちは物質のふるまいについて深い理解を得ることができました。
まさに、最先端の研究の礎となっているのです。

だからこそ、今回ノーベル物理学賞に選ばれたのでしょう。

おっと、感動に浸っていて忘れていました！！　このブログは連載企画でしたね！！
まだ、「わかった！山」はあと2つも残っています！
今回の山は、まだまだ序の口。
次の山からはもっと険しい道のりですよ......！

とはいえ今回は、お疲れさまでした！

「わかった」への相転移
（リンクは削除されました。また、URLは無効な場合があります。）

　① ブログリレーでもう一度解説します
　② 2次元での相転移を説明したKT転移（この記事）
　③ 1次元ではもっとすごい相転移が起こる
　④ 量子ホール効果をトポロジー