皆さんこんにちは。少しでも未来館に数学を、ということでコソコソ活動している科学コミュニケーターの鈴木です。
数学は身の回りのいろいろなものに応用されています。それだけでなく、数学にはまだはっきりと解明されていない、奇妙な性質や不可思議な類似など面白さもたくさん隠れています。しかし、数学というと、未来館という場所であってさえ、あまり反応がよくありません。
皆さんは、数学は好きですか?
そんなこと考えたこともないという人や、数学はそれほど好きではないという人でも、「ちょっと数学おもしろそう」と思ってもらえそうなものをこのブログで目指したいと思います。
1.方程式の中のそっくりさん
小学校までに皆さんも「1、2、3、4、・・・」のような普通の数字を覚えたと思います。そのあと小学校で分数や小数が出てきます。やがて、中学に進むと√2や円周率などの無理数と呼ばれる数がお目見えします。そして、高校では虚数記号「i」の登場です。同じ数を二度かける(二乗する)と「-1」になるという、取り出して見ることのできない数です。無理数までの数と違い、目に見えず、数遊びのように思える虚数ですが、実は物理学でも一般的に使われ、私たちの世界の現象を説明することができる数となっています。
しかし、逆に、「目に見える数」というのは本当にこの世界の現象を表しているのでしょうか?
それでは、虚数や普通の数の裏にある目に見えない別の数の世界をお見せしましょう。
中学校で習った二次方程式を覚えているでしょうか。覚えていなくても良いです。例えば、次のような式を満たすxを求めろという問題です。
![]()
この解はx=1, 3ですね。二次方程式をより一般的に書けば下のようになります。

中学校で何度も計算した方程式ですが、昔の数学者も同じように二次方程式を調べ、解いていました。そして、中学で習うように、二次方程式には解の公式が見つかっています。
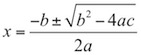
覚えていなくても良いです。
この式を奇妙に思ったことはないでしょうか。
そう、二つの解の形が似ていますね。二次方程式の二つの解はプラスとマイナスが一か所入れ替わっただけです。
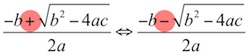
例えば、解がx=1, 3の時でいえばx= 2-1, 2+1と書けるわけです。
もしかしたら、二次方程式の解の公式の求め方を覚えている人は不思議に思わないかもしれません。でも、三次方程式ではどうでしょうか。
三次方程式の解はカルダノの公式によって求めることができます。三次方程式というのは以下のような式です。
![]()
この方程式をカルダノの公式によって解くと以下のような解が得られます。
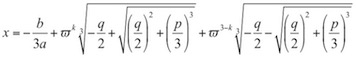
(※ k=1,2,3それぞれを代入した3つが解です。p, qはa-dで求まる定数ですが、複雑なので省略しました)
どうでしょう。これも三つの解が互いにそっくりですね。複雑に見えますが、ω以外は定数です。ωは1の三乗根のうち1でないもののことで、以下のように表されます。
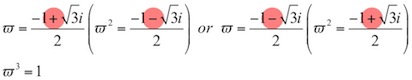
カルダノの公式にはωの一乗、二乗、三乗が出てきますが、1になるかプラス・マイナスを入れ替えるだけのそっくりな形になることがわかります。
こうなると四次方程式以上でもどうなのかが気になりますね。四次方程式の解はフェラーリの公式などで求まります。
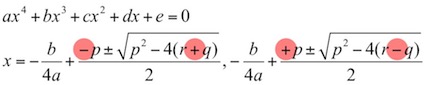
(p, q, rはa-eで求まる定数です。かなり複雑なので省略しました)。
やはりそれぞれ記号を入れ替えただけのそっくりな形になっていますね。
そして数学者たちは五次方程式の解の公式も求めようとしました。五次方程式の解もどのようになっているのか気になりますね。しかし、たくさんの数学者の挑戦をはねのけ、五次方程式の解の公式はなかなか求められませんでした。
実は、五次方程式の解の公式はないのです!(*1)
この事実を発見したのは、パオロ・ルフィニ、ニールス・アーベル、エヴァリスト・ガロアなどの数学者であり、19世紀初頭前後に研究されました。
特に、ガロアが見つけた理論を使えば、五次方程式以外についても、解を書き表すことができる方程式の特徴や解のかたちを知ることができます。これは「ガロア理論」と呼ばれます。ガロア理論によって方程式を解き明かすには、方程式の性質を表に書き表したような「ガロア群」を使います。(*2)方程式をあらゆる日本語だとすれば、ガロア群はあいうえお表みたいなものです。
ガロア群はいまだに全貌が明らかになっていません。しかし、それがわかれば謎の多い方程式の世界や数の性質などが解き明かせます。そのため、見つかってから180年以上経過していますが、今なお研究されています。
実は、この研究の中に、「この世界の裏側にある数」への扉がひそんでいます。
2.ガロア群と右左ひっくり返った数
ガロア群を直接すみずみまで調べるのはなかなか難しいので、部分的な情報を持った別の群(前述の言葉で使うと、濁点を付けられる文字だけを取り出したあいうえお表のようなもの)を探して研究するという方法をとっています。
なかなかの回り道です。実はこの研究分野で出てくる「部分的な情報を持った別の群」の一つが「p進数」なんです。
急に出てきたようなp進数ですが、実は過去の数学ブログで取り上げていました。覚えている方はいるでしょうか。
・「円周率の日々」数字を無限に並べて計算してみたら(完全版)(2019年03月15日)
https://blog.miraikan.jst.go.jp/other/20190315post-844.html(リンクは削除されました。また、URLは無効な場合があります。)
この記事を読まなくても下を読み進められます。「p」というのは素数(Prime)だということだけ覚えていてもらえれば大丈夫です。
このp進数こそが「この世界の裏側にある数」と呼べるものです。
まず普通の数は、「1」や「100」や「9999999999」や「0.001」や「3.14159265」があります。「0.9999999...」といった無限小数もありますね。(分数はおいておきましょう)
普通の数は、桁が左に増えるにつれて1倍、10倍、100倍と絶対値が大きくなります。逆に小数点から右に増えるにつれて、1/10倍、1/100倍と絶対値が小さくなります。
これに対して、p進数は逆になります。左右ひっくり返っています。
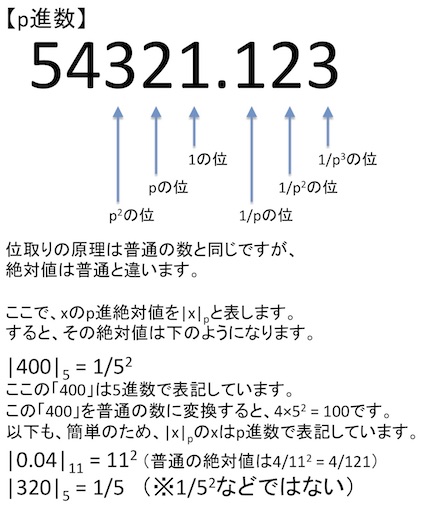
p進数の絶対値は、桁が左に増えるにつれて、1倍、1/p倍、1/p^2倍と小さくなり、小数点から右に増えるにつれて、p倍、p^2倍と大きくなります。(*3)なんでそうなるのと思われるかもしれませんが、これはそのように決まっている定義です(混乱してきた方は、とりあえず、ひっくり返っていると思っていてください)。
p進数には「1」や「100」や「9999999999」や「0.001」や「3.14159265」があります。似ているというか、同じですね。違うのは無限小数というものはなく、逆に左に無限桁の数があります。「...9999999.9999」のようなものです。
3.この世界の裏側にある数
これまでに見たように、p進数は性質が普通の数とひっくり返っていました。しかし、「この世界の裏」にあるというのはどこにあるのでしょう。
実は、私たちが普段使っている数とp進数は表裏一体となっているという公式が存在するのです。それは「積公式」と呼ばれ、ある数の普通の絶対値とp進数に変換した絶対値をすべて掛け合わせると「1」になるというものです。(*4)
何かの長さを測ったり、体積を量ったり、時間を計ったり、普段は普通の数字で読んでいますが、実はその裏には常にp進数が存在しています。そっちの数のほうが本当と見ることもできるかもしれません。

宇宙の物質はすべて素粒子からできていると物理学では考えますが、そもそも、それを測定して見ている数字は私たちが普段使っている数よりもp進数で読み取るべきなのかもしれません。この宇宙の物理法則はp進数で書かれているのかもしれません。現在では、p進量子力学などと呼ばれ、研究が進んでいます。
4.p進数論の研究者
そんなp進数論を研究している数学者のひとり、三原朋樹先生にお話を伺いました。三原先生は筑波大学で研究をされ、p進数論を使ったガロア群の研究や、人工知能への応用にも取り組んでいます。以下のインタビューでは、三原先生のお人柄がよく表れていましたので、ほぼ先生の口調のまま、お届けしております。
Q1. 好きな数字はありますか?その理由は何ですか?
A. 2進数を考えているときは2が、3進数を考えているときは3が、5進数を考えているときは5が好きです。
それらがp進数のさまざまな性質を支えているからです。
Q2. 好きな数学の公式、補題、予想はありますか?それのどんなところが好きですか?
A. たくさんありますが、例えば等比数列の和の公式1+r+r^2+...=1/(1-r)(|r|<1)はとても面白いと思います。
最初に習う頃はrが絶対値1未満の実数として習いますが、大学で数学を学ぶともっと広くrが絶対値1未満の複素数でも良いことがわかったり、
更に広くノルム(絶対値のようなもの)が1未満の複素正方行列でも良いことがわかったり、
かと思ったら単に広がっていくだけでなく別の方向で絶対値が1未満のp進数でも良いことがわかったり、
「一般の可換環における冪零元」というものでも良いことがわかったり、
「一般の可換環を係数とする定数項を持たない形式冪級数」というものでも良いことがわかったり、
「一般の可換環Rとその部分環SとそのイデアルIであってIの冪乗が生成するSの可換環としての位相が完備であるようなものに対し冪乗がIに属するRの要素」
というものでも良いことがわかったり。
好きなだけ抽象化することが出来ます。ただ抽象的になるだけでなく、いろいろ面白い側面もあります。
例えば2進数の場合、2はp進数としての絶対値が1/2なので1未満ですからこの公式のrに代入することができます。すると1+2+2^2+...=-1という式を得ます。実数としてなら発散してしまう左辺も、2進数としてなら何の問題もなく収束します。さらに左辺をp進法で表記すると、1+10+100+...となるので、これは右の桁から順番に筆算すると、...111となります。
つまり等比級数の公式は2進数のよく知られている等式...111=-1も与えています。計算機に慣れている人なら、この等式を見て「補数表現」という実用的な概念を思い浮かべるかもしれません。
この公式は正方行列に対してもp進数とはまた違った面白い側面がありますが、今回はp進数のお話ということでそこは割愛させていただきます。
Q3. 好きな数学者はいますか?その理由は何ですか?
A. 辻雄先生とPeter Schneider先生を心から尊敬しております。(鈴木注:お二人ともp進数論の研究者です)。お二人には大学院在学中に懇切丁寧に指導していただき、のびのびとさまざまな数学を学ばせていただきました。
Q4. どんな人(どのような職の人)に数学を好きになってもらいたい、使ってもらいたいと思いますか?その理由は何ですか?
A. どんな人にも数学が好きになっていただきたいです。趣味でも、仕事に役立てるのでも、どんな形でもいいので数学を好きな人や使ってくれる人が増えてくれればと思います。
自分の好きなものを、他の人も好きになってくれることはとても嬉しいですからね。数学が好きになってくれる人が増えて、あわよくば数学者を志す人が増えてくれたら、難しい問題を一緒に考えてくれる仲間が増えることになるのでさらに嬉しいです。
Q5. どんな分野に数学を応用してみたら面白いと思いますか?
A. すでに数学が応用されている(または逆に数学からもある意味応用させてもらっている)分野が多いと思いますが、個人的には人々の暮らしに直接つながる分野、例えば医療とか建築業とか通信機器・計算機や自動車・航空機等の産業とか、そういった分野に今後も数学が応用され続けていってくれたらいいなと思います。
私たちの身近なところには、私たちが見えないところで色々な数学が応用されています。人々がなるべく不自由なく暮らしていけるよう、私たちの数学が陰ながら支えていけたら素晴らしいことだと思います。
もちろん、あまりに生活に溶け込みすぎてまったく気付かれなくなってしまって見向きもされにくくなってしまったら元も子もありませんから、適宜「こんな素晴らしい数学が使われていますよ」とか「この数学にはこんな可能性があると思いますよ」とか自己主張していきたいです。
いかがだったでしょうか。方程式の解のきれいさを調べた歴史、普通の数とはルールがひっくり返ったp進数、それがこの世界の見え方もひっくり返すかもしれません。
数学は奇妙な性質もたくさんありますし、数学そのものや物理学以外にも応用の例がたくさんあります。皆さんのそれぞれの分野で数学が役立ったり話のネタになったりする機会があると思います。この記事と三原先生へのインタビューから、少しでも数学を面白そうと思っていただけたら嬉しいです。
たまには数学もいいですよね。
5.補遺
*1 四則演算と冪根で書き表すことはできないという意味です。他の表記を使って五次方程式の解を求めるとすれば、三角関数や積分、楕円関数やモジュラー関数などを使う公式があるようです。
*2 この記事で「ガロア群」と呼んでいるものは絶対ガロア群です。ここでの絶対ガロア群とは、有理数体Qに新しい要素(無理数など)を追加していき、ガロア群をどんどん拡大したとき、これ以上拡大できないという状態のものです。ものすごく大きくて複雑なので今もなお研究対象となっています。
*3 普通の絶対値は普通の数のプラス、マイナスの符号をとったものですね。+5の絶対値は5、-3の絶対値は3です。
一方、p進絶対値は、素因数分解をしたとき素数pの何乗を含んでいるのかを見ます。75であれば、3×5×5、105であれば3×5×7です。ここで、75の素数5のp進絶対値は1/25、105は1/5になります。注目している素数の積をたくさん含むほどp進絶対値が小さくなることがわかると思います。5進数320は、普通の数にすると3×25+2×5+0 = 85 = 5×17となり、素因数5は一つだけ含まれます。つまり、5進絶対値は1/5になります。
*4 積公式は、普通の数の絶対値とp進絶対値がわかれば簡単な公式です。積公式では、普通の絶対値とあらゆる素数についてのp進絶対値をすべて掛け合わせます。つまり、75や105であれば以下のようになります。

これがいつも「1」になることは直観的にわかると思います。







