みなさん、こんにちは!メディアラボ17期「数理の国の錯視研究所」研究所員(自称)こと、科学コミュニケーターの片平です。
残念ながらメディアラボ17期は5月15日をもって終了となってしまいましたが、5月13日には「数理の国の錯視研究所」への出展者のお一人、明治大学先端数理科学インスティテュート特任教授 杉原厚吉先生をお迎えしてサイエンティストトークを行いました。このブログではイベントの模様とそこで参加者のみなさんにも取り組んで頂いた錯視作品の制作方法をご紹介します。
前回のブログ錯視つくってみた、の進化版、みなさんも錯視つくってみて、です。
最後まで読んでいただくと、こんな錯視作品が自分で作れるようになります!

参加していただいたみなさんには会場でお約束した通り、ブログの最後に作品の展開図をご紹介しますので、最後までおつきあい下さい。
さて、まずはサイエンティストトークの様子をご紹介します。「数学」と聞くと少し苦手意識を持ってしまう人もいるかなぁ、と心配しましたが、写真の通り、多くのお客様に集まって頂きました。

では、トークの内容をご紹介していきましょう。
1.どうして錯視がおきる?
どうして錯視は不思議に見えてしまうのでしょう?
今回扱う錯視の原理は、ひとつの画像を見たときに「数学的には無限の可能性があるが、人は特定の立体しか思い浮かばない」ということを利用したものです。
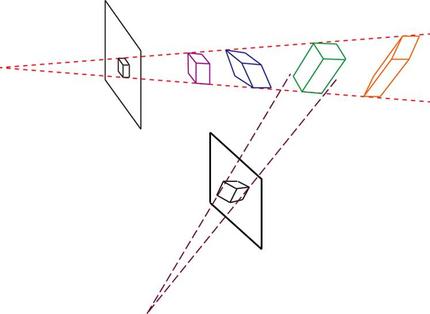
下の図を見てみましょう。画像に描かれた立体を見たとき、これはどんな形をしているか?と想像すると、多くの人は、直角が集まってできた形、紫の立体を思い浮かべると思います。(もちろんそう見えない人もいます!)ですが、赤い点線を通る位置に頂点を持っている立体はどの立体も同じ形に見えます。画像には奥行き(下の図では左右方向)の情報が失われているので、その違いはわかりません。

ここで作ってもらう錯視もこの奥行きを上手く利用した錯視です。名付けて「奥行きであざむく」錯視です。
この「奥行きであざむく」錯視の作品を見て頂くと、説明を聞いて、仕組みがわかっていても、やっぱり不思議に見えてしまうことに、みなさん驚きです。私も、いえ杉原先生でさえも、やっぱり不思議に見えてしまうそうです。
2.錯視を作るのは数学?
ある視点から見たときに画像と同じように見える立体は、頂点が点線(赤)の上を通る立体であることがわかります。この、「点線の上を通る」という条件は数学の言葉を使うと、方程式で表せる、ということができます。
そして、別の方向から見たときも同じように方程式であらわすことができます(紫の点線)。この2つの方程式からなる、連立方程式を解くと、望みの立体を創ることができます(緑の立体)。2つの方向から見てそれぞれの形に見える立体を創作することができる。直観でつくるのは難しいのです。
ここまで話をすすめていくと、会場には、「?」の文字がちらほら......。2つの方程式?連立方程式?いえいえ、大丈夫です。今回は方程式を解く代わりに作図で錯視を作っていきます。(作図で解くことは杉原先生のご専門「幾何学」という分野の考え方でもあります。)
3.錯視を数学で作ろう!
さて、2つの方向から見てそれぞれの形に見える立体を創作することができる、とわかったところで、実際に作ってみます。最初に写真で見てもらった通り、片方から見ると四角形、もう一方から見ると三角形の立体を作ります。
手順は、次の通りです。ワークシートを見ながら、挑戦してみて下さい。実際に作図をするためには作業シートを使って下さい。ワークシート.pdf 作業シート.pdf
- 見えて欲しい形を平面に描き(平面図)、断面a、b、cをつくる。
- 垂直面aを横から見た図(側面図)に四角形の頂点と三角形の頂点に見えて欲しい空間の点を作図する。
- b、cも同じように作図する。
- 側面図の上で求めた空間の点を、平面図にも描く。
- 平面図で点をつないで、柱体の断面図(真上から見た形)を作る。
- 側面図で点をつないで、柱体の上面の側面図(真横から見た形)を描く。
- 側面図に垂直方向の長さが一様な柱体側面を作図する。(垂直方向の長さは自由)
- 平面図と側面図から、柱体の展開図を作図して立体をつくる。
先生が順番に説明していきますが、会場のみなさんも作業シートに向き合って、真剣そのもの。特にお子さんよりもお父さんが夢中な姿が印象的でした。会場からは、頭の普段使わない部分を使っている気がする~、なんて声も。
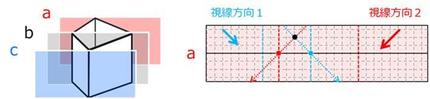
ここでは、この錯視のポイントである2について作業シートの一部を見ながら、説明します。
上で説明した「奥行きであざむく」を思い出して下さい。
視線方向1から見ると、四角形にみえる立体を作ろうとしています。平面で四角に見える形はひとつではなく、「奥行きであざむく」ことで無限の可能性があるのです。
つまり、側面図aに見える四角形の頂点は平面上では青い点の位置に見えますが、青い点線上ならどこにあったとしても、視線方向1から見れば「奥行きであざむく」ことで四角形の頂点に見えるはずです。この斜めの点線が四角形の頂点を表す方程式、ということになります。
同じように赤い点、つまり三角形の頂点と視線方向2の関係を考えてみましょう。
やはり、赤い点を通る赤い点線上のどこに点があったとしても視線方向2から見れば、三角形の頂点に見えるように「奥行きであざむく」ことができます。こちらも同じように斜めに描かれた線が方程式、ということになります。
すると、視線方向1から見ると四角に見えて、視線方向2から見ると三角に見える、この2つを満たす点がみつかります。それは、2つの点線が交わる点です。これが2つの方程式からできる連立方程式を解いた、ということになるのです。
ぜひ、ワークシート、作業シートをダウンロードして自分で作ってみて下さい!
4.数学のチカラ
さて、錯視作りに挑戦してくれるみなさんはすでに錯視研究所の一員です!この錯視が作図によって作れることをぜひ体感してみて下さい。
不思議な錯視を自分で作りたい!という願いを数学が実現してくれました。
こんな風に数学を使うことで、解決したい問題やほしいものといった現実を数学の問題に置き換えることができます。そして解いた数学の答えから実際の問題の解決方法やものづくりのヒントを得ることができるのです。
そう考えると、数学の問題を解くのも、錯視の作品を作ってみたり、みなさんの願いを叶えるための方法を探ったり、そんな風に感じられるのではないでしょうか。ぜひ、色んな場面で、数学のチカラを発揮してください!!
会場でのアンケートでも、ちょっと難しい、と感じたけれど、自分で考えて作れることに満足した。楽しかった。と言ってくださるお客さんが多かったようです。難しいな、と思うことを実現するチカラ、それが数学のチカラだと思います。数学のチカラを実感していただけて本当によかったです。参加してくださった皆さま、ありがとうございました!
最後に、それでもやっぱりどうしても、という方のために。
展開図はこちら。(答え)展開図.pdf








