
こんにちは!
坪井からバトン (リンクは削除されました)を受け継ぎました、ぶつりーずの雨宮です。
いよいよブログリレーも今回でおしまいですね...!嬉しいような、寂しいような。
さあ、「わかった山」への最後の登頂となる今回の内容は、2016年ノーベル物理学賞の3本柱の最後の1つ、サウレス博士による「量子ホール効果のトポロジーによる説明(TKNN整数)」のお話です!
...と、難しい言葉を聞いても、だんだん動じなくなってきたのではないでしょうか?
うんうん、わかります。
――そして!
いままで「KT転移山」と「ホールデン予想山」を登ってきた精鋭のみなさま、そしてもちろん今回初めてこのブログリレーを見るみなさま、ご注意あれ!
今回登頂する山は、もはや山ではありません。これは「崖」です。
理解するのにはとっても苦労するし、実際まだ私も崖登りしている途中です(でもちょっと見えてきた)。
ただ、登山、いや崖登りに苦労する分、その先にはサウレス博士が見晴らしを利かせてくれた物理学の景色が、きっと見えるはず。
その景色を見るべく、一緒に登って行きましょう!
では、登るコースを考えましょう。
このブログリレーでは、ディープな話をできるだけ「わかった!」と言っていただけるよう、そもそもの背景からていねいに積み上げることを大事にしてきました。
もちろん最後の最後まで、ていねいに登っていきますよ。ということで、本日の登山コースはこちらです↓↓
本日の登山コース
1合目:山の名は
2合目:ホール効果はヨコ抵抗!
3・4合目:とびとびの値。ランダウ量子化!
5~7合目:量子ホール効果の発見、そしてノーベル賞
8・9合目:サウレス博士登場!トポロジーで説明
10合目:サウレス博士が見せてくれた景色
1合目:山の名は
まずは「今日登るはどんな山か」から考えていきましょう。
山内が説明したKT転移 (リンクは削除されました)は「2次元」、そして坪井が説明したホールデン予想 (リンクは削除されました)は「1次元」の物質のふるまいについてでした。
そして今回の山はというと...「2次元」のお話です。その名は「(整数)量子ホール効果」!
ただ、ちょっと待って!この「量子ホール効果」自体をサウレス先生が発見した訳ではないのです。
...実はこの現象はドイツの物理学者クラウス・フォン・クリッツィング博士が1980年に発見し、1985年にノーベル物理学賞を受賞しています。これだけでも一つの大きな「山」なのですが、サウレス先生が到達したのはその山の上からさらに天空へと続く崖の上です。
いきなりサウレス先生が到達した場所へとショートカットで行くことはできないので、まずは一番ふもとからじっくりと、そもそも「量子ホール効果」とは何だったのか?というところから皆様と一緒に登ってみたいと思います。
今回紹介する現象が起こる「2次元」の舞台とは、具体的には「半導体と半導体の間の2次元」のことです。

これが今日の舞台(の一例)である、半導体を合わせた基板の図です。ヒ化ガリウムGaAs(電子機器に使われる材料の一つです)も、それにアルミニウムを加えたAlGaAsも半導体(電気を通す導体と電気を通さない絶縁体の中間の性質を持つ物質)の一種で、それらが合わさっていますね。
(実際にはヒ化ガリウムなどに限らずさまざまな材料で、これからお話しする整数量子ホール効果という現象が起こることが確認されています。)
上の図のような組み合わせのとき、上の半導体は下の半導体に対して電子を供給しますが、電子が下の半導体に移動すると、静電気的な力によって上の層に引き戻されようとします。その結果、電子は半導体と半導体の間の面(←2次元!)だけを動く、ということになるのです。
その「2次元の電子の動き」が、今回のポイントです。
2合目:ホール効果はヨコ抵抗!
では、先程の図を上から見てみましょう。
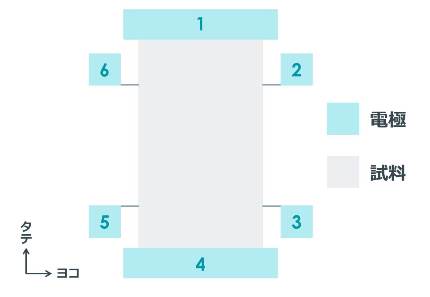
ちょっと特徴的なカタチをしているこの試料は、「ホールバー試料」といいます。1~6という数字がついた部分は、電極です。電圧や電流を調べるためにつけてあります。
さあ、このホールバー試料の1番と4番の部分を電池につないで電圧をかける(電場をかける)と、電流はこのように流れます。
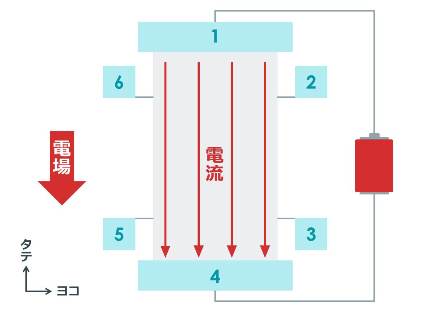
ここで、「抵抗の値」を計算してみましょう。
使うのは、「オームの法則」と言われる次の式です。
(抵抗)=(電位差)÷(電流)
例えば電極2と3の間を見てみましょう。電流の流れを川の流れに例えると、2番の方が電流が流れてくる「上流」にあたり、3番の方が「下流」になります。そしてその上流と下流の高さの差を「電位差」とよびます。例えばその値が30Vで、電流が3A流れているとしたら?
――抵抗値は30÷3で、10Ωになります。
...いやいや、これって中学校の時にやったよ。普通じゃん!という方もいるかと思います。
実はそうなんです!ここまではいたって普通なんですが、今回のテーマのおもしろさはここからなんです!!
そもそも「電流」というのは、「電」子の「流」れです。
そして、電流の向きと電子が流れる方向は、実は反対なので、先程の図だと、電子の流れはこのようになっています。

ここで、電源からの「電場」だけではなく、ホールバー試料の奥から手前に突き抜ける方向に、非常に強い「磁場」もかけていきましょう。
すると電子の動き方は...?

あっ、電子が曲がって動いた!
...そうなんです。強力な磁場をかけると、電子は試料タテ方向に進むは進むのですが、同時に「ヨコ方向」にも流されるのです!
――これは、電荷を持った電子がローレンツ力を受けるため。中学の時に習ったフレミングの左手の法則を考えると納得できると思います。
もちろん試料中を流れる電子の数は1つではないので、たくさんの電子がヨコ方向に流れます。

その結果、電荷がかたよってしまっていますね。
例えば、電極2と6を見てみると、磁場が無いときには電位差が無かったのですが、磁場によって起きた電荷のかたよりによって、「ヨコ方向にも電位差が存在する」ことになります。このことをホール効果といいます。
その電位差をさきほどのオームの法則に当てはめてみると、
(ヨコ方向の抵抗)=(ヨコ方向の電位差)÷(電流)
つまり、「試料のヨコ方向にも抵抗値が存在する」ことになります!(このヨコ方向の抵抗を「ホール抵抗」と言います)
この、電子をねじ曲げる力は磁場が強いほど大きくなるので、実際ホール抵抗も磁場とともに滑らかに大きくなって行きます。しかし、ある条件まで達すると、その値が「とびとび」になってしまうのです!これが「量子ホール効果」です!!
今回のテーマ「量子ホール効果」をごくごく簡単に言うと、「極低温、強磁場の条件のもとで、抵抗の値がとびとびになる」となるのですが、この時の「抵抗」とは、今紹介したヨコ方向のホール抵抗のことなのです!(いつものタテ方向の抵抗のことじゃなかった!!)
3・4合目:とびとびの値。ランダウ量子化!
「抵抗の値がとびとびになる」...?
いったいどういうことなのでしょうか?それを知るために、電子についてもっと正確に考えていきましょう。
磁場がかかった状態で電子が動けば、ローレンツ力で進行方向ヨコ向きに力がかかる、というのは先程の説明なのですが、
「進む」→「力がかかる」→「曲がってすすむ」→「そのさらに横向きに力がかかる」→「さらに曲がる」→...
これを繰り返していくと、電子はこのようにぐるぐるとまわり出します。(円運動の半径を、サイクロトロン半径といいます。)

...もう勘のいい方は気づいたでしょうか。
実は先ほどのホールバー試料の中を進む電子は、正確にはこのように「ぐるぐる回転」しながら、「ヨコ方向」に進んでいくのです!

ただ、この「ぐるぐるの動き」にはある重要な特徴があるんです...。
磁場の強さを強くすれば、ローレンツ力も強くなるので、サイクロトロン半径は小さくなります。(くるくるくるくるくる...)
反対に、磁場の強さを弱くすれば、サイクロトロン半径は大きくなります。(ぐーるぐーる...)
ここまではいわゆる古典的な力学で説明できるのですが、これからはさらに進んだ物理、量子力学お話になります。
量子力学によれば、電子は波の性質も持っているので、磁場が強くなってサイクロトロン半径が電子の波長と同じくらいの長さに近づいてくると、とびとびの値しかとれなくなってしまいます。
このことを「ランダウ量子化」といって、「サイクロトロン半径がとびとびなので、そのときの電子が持つエネルギー(サイクロトロンエネルギー)がとびとびになる」ということを表しています。この「とびとび」な性質は温度が低くて磁場が強いほどはっきりしてくるのですが、その「とびとび」が量子ホール効果の実現に重要なのです。
5~7合目:量子ホール効果の発見、そしてノーベル賞
ここまでお疲れさまでした。やっと半分まできましたね!
この5~7合目では、とびとびなエネルギーをもつ電子が見せる不思議な現象を紹介します!個人的にはここの現象が最も「おお...おおおお!」となったところです。
条件をおさらいしましょう。
いまは、「非常に強い磁場」と「極めて低い温度」で、ホールバー試料に電場をかけて電子を動かしているところです。
このホールバー試料にかける磁場を徐々に強くしていって、タテ抵抗とヨコ抵抗の値を調べてみると、こんなグラフになります。
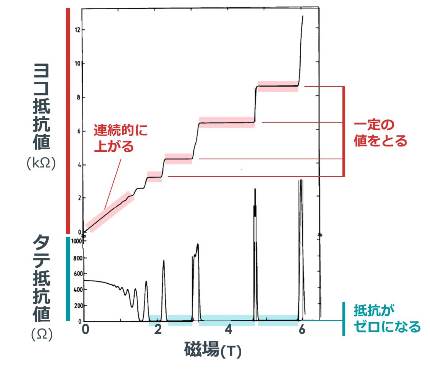
まずはヨコ抵抗のグラフに注目してください!
磁場が0T~1Tのとき、磁場を強くすればするほど、ヨコ抵抗は連続的に上がっていくように見えます。
では磁場が1T以上のとき、磁場を強くすればするほど...あれ?
(特に4Tあたりがわかりやすい)磁場を強く...えい!...強く...えい!えい!...むむむ、磁場の強さを (ある程度) 変えても、ヨコ抵抗が上がらない!!
もっと磁場を強く...えいえいえい!!...(5Tより少し弱いあたり)...おおお!一気にヨコ抵抗値が上がった!と思ったらまた一定になってしまった...!!
いかがでしょうか?グラフからわかる通り、「普通に考えたら磁場を強くすればするほど連続的に抵抗は大きくなる」のですが、実際は「ヨコ抵抗値は階段状に変化」しているのです!!
(おお...おおおお!)
しかも!
階段状になっている部分の抵抗値は、こんな式で書き表せます。
R = 25812.807/n (Ω) (n=1,2,3...)
なんと、階段の高さは適当なのではなく、非常に正確な値(7~8桁以上の精度)を、整数で割った値になるのです!
(おお...おおおお!←2回目)
しかもしかも!
ヨコ抵抗値が一定になっているときの、タテ抵抗値をご覧ください。
なんと!抵抗値がゼロになっています!
つまり、超伝導のように、電子のエネルギーが下がることのないままタテ方向に流れるということです!
(※正確には、タテ方向に進む電子は、ホールバー試料の中心は流れず、両端のみ流れます。)
(おお...おおおお!←3回目)
この現象は、「整数量子ホール効果」というもので、ドイツの物理学者クラウス・フォン・クリッツィング博士が1980年に発見し、1985年にノーベル物理学賞を受賞しています。
8・9合目:サウレス博士登場!トポロジーで説明
さあ、いよいよ8合目。だんだん山の頂上が見えてきましたよ...!
ここまでは整数量子ホール効果についてじっくりと説明してきました。「ノーベル物理学賞」という言葉は出てきましたが、今回受賞されたサウレス博士ではなく、クリッツィング博士の功績でした。
では、サウレス博士は整数量子ホール効果について、何をしたのでしょうか?
整数量子ホール効果がなぜ起こるのかを説明する方法はいくつかあり(※1)、ミクロな電子の運動からこの現象を説明することはできていました。それを「トポロジー」に結びつけて、一段高いところから物理現象を見渡す道を拓いたのが、サウレス博士達の研究だったのです!(やっと「トポロジー」が出てきた...!)
サウレス博士は、ヨコ抵抗(ホール抵抗)の逆数であるホール伝導度σが、

という、いたってシンプルな式で表されることを導き出しました。この公式を、研究者のサウレス博士・甲元博士・ナイチンゲール博士・デンニイス博士の頭文字をとって、「TKNN」公式といいます。
このTKNN公式の「e」というのは電子が持っている電荷の大きさ、「h」というのは「プランク定数」といって量子力学で出てくる基本的な定数で、どちらも自然界の基本をなす、大事な数字なのです(このこと自体はクリッツィング博士もすでに指摘していました)。そして一番重要なのが、この「ν」と書かれている部分です。これは「チャーン数」という整数で、トポロジカル不変量の一種です。KT転移で登場した「トポロジカルチャージ」と同じように、このチャーン数も整数の値しか取りません。だからこそ、ホール抵抗が"とびとび"になるのですね!
※チャーン数は、数学(位相幾何学)で使われる空間の性質を特徴づける量の一つです。ここでは電子が運動を記述する空間を特徴づけます。
つまり、とびとびになる抵抗値の謎が、トポロジカル不変量によって説明できたのです!!この偉業が認められ、今回のノーベル物理学賞で、サウレス博士の功績の一つ、いやむしろ最も重要なテーマとして取り上げられたのです!
10合目:サウレス博士が見せてくれた景色
やっと10合目到達!ここまで読破いただいた皆さん、お疲れさまでしたー!
さあ、最後の10合目では、サウレス博士によってつくられた「TKNN山頂」からの絶景を見てみましょう。
絶景ポイント①:「抵抗標準」になりうるほどの正確さを持つ整数量子ホール効果
5~7合目でも書きましたが、整数量子ホール効果で現れる抵抗値は、恐ろしいほど精度の高いものでした(試料のサイズや物質、作製条件によらず、一定値をとるという意味で)。
その精度の高さから、「電気抵抗そのものを、整数量子ホール効果を使って再定義しよう!」という動きがあり、もしかすると近い将来、量子ホール抵抗値が、電気抵抗の定義となるかもしれません。
※現在の直流抵抗標準は量子ホール効果によって実現されています。
それほどに重要な現象を説明したのが、サウレス博士だったのです。
絶景ポイント②:磁場なし条件下での整数量子ホール効果
今までの整数量子ホール効果は「強い磁場がかかったとき」という前提がありましたが、サウレス博士の功績をさらに発展させ、「磁場がないところでも 整数量子ホール効果を表すモデル」を考案したのが、ホールデン博士です。
(ホールデン博士は、前のリレーブログで紹介した、今回の受賞者の一人、ダンカン・ホールデン博士です。)
そのモデルがさらに発展し、現在たくさんの研究者が取り組んでいる「トポロジカル絶縁体」の研究にもつながっていきます。
トポロジカル絶縁体についてはこちらのブログ (リンクは削除されました)をご覧ください。
絶景ポイント③:トポロジカル普遍量から物理現象を予測する
以前の記事で説明したKT転移では目に見える形の「渦」がトポロジー的な性質を担っていました、しかしサウレス博士が提案したのは、数学的に導入されたトポロジカル普遍量であるチャーン数を利用して物質全体の電気的な性質などを説明するということをやってのけたのです。
この発見以降、何らかのトポロジカル普遍量に結びつけて分類することで、物理現象を予測することができるようになりました。
もともと数学の世界で使われていた概念を、物理学の世界に持ち込むことに成功したサウレス博士の研究は、まさに、新しい世界を切り開く道しるべになったのです!
サウレス博士がTKNN公式を発表したのは1982年のことですが、その成果が、たくさんの研究者の礎となり、未来の社会につながっていくと考えると、改めてその偉大さがわかります!
ブログリレー最後の山である「TKNN山」(もはや崖)はいかがだったでしょうか?
個人的には、2015年のノーベル物理学賞「ニュートリノ振動の発見」は純粋におもしろかったのですが、今年のトポロジーは理解するのに本当に苦労しました。ちょっとやそっと勉強しただけでは私の中での「わからない」状態は変化せず、でも「えい!えい!」と取材したり、本を読みあさったりして、ある瞬間に一気に「わかったー!」状態へ変わる。 ――そんな「わかった」への相転移のような経験をするきっかけに、このブログリレーがなれたなら、こんなに嬉しいことはありません。
また、ここまで読破頂いたみなさまとともに、ブログリレーを書くにあたり、取材や質問をさせて頂いた研究者の方々にも改めて感謝申し上げます。
「わかった」への相転移
①ブログリレーでもう一度解説します (リンクは削除されました)
②2次元での相転移を説明したKT転移 (リンクは削除されました)
③1次元ではもっとすごい相転移が起こる (リンクは削除されました)
④量子ホール効果をトポロジー (この記事)
(※1)整数量子ホール効果の説明として、トポロジカル不変量による説明のほかに、端状態による説明や、ラフリンの思考実験などがあります。詳細は参考文献[1]
参考文献
[1]勝本信吾『新物理学シリーズ43 半導体量子輸送物性』培風館 2014
[2]"Klaus von Klitzing - Nobel Lecture: The Quantized Hall Effect". Nobelprize.org. Nobel Media AB 2014. Web. 28 Nov 2016. https://www.nobelprize.org/nobel_prizes/physics/laureates/1985/klitzing-lecture.html
このブログ記事の作成にあたり、理研・創発物性科学研究センター研究員の川村稔さん、そして同研究センター研究員で、未来館の47期ボランティアでもある中島多朗さんに多大なご協力をいただきました。誠にありがとうございました。




